Физические предпосылки. Полная энергия и волновая функция молекулы в адиабатическом приближении. Какую роль для ядер играет энергия электронного облака. Функция потенциальной энергии ядер, различные ее формы. Равновесная конфигурация. Почему для устойчивости молекулы потенциальная функция ядер должна иметь форму ямы?
Конформеры, эксимеры, молекулы с внутренним вращением, молекула аммиака NH3.
Порядок величин элетронного, колебательного и вращательного движений молекулы. Качественная оценка величин энергии.
Энергетическая диаграмма двухатомной молекулы. Основное и возбужденные электронные состояния.Обозначения электронных состояний.
Электронные, колебательные и вращательные спектры и диапазоны длин волн, в которых они расположены.
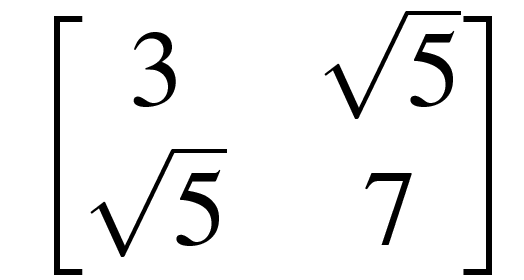
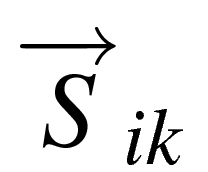 .
.