Электронный парамагнитный резонанс (ЭПР). Ядерный магнитный резонанс (ЯМР).

Предварительный опрос

  • Что такое угловой момент.
  • Что такое магнитный момент.
  • Что такое спин.
  • Чему равен спин электрона.
  • Сложение моментов количества движения в квантовой механике.
  • Обозначение состояний электронов атома. Правила Хунда.

Содержание лекции

  • Определение магнитного момента.
  • Момент количества движения.
  • Связь магнитного момента с орбитальным и спиновым моментом количества движения. Магнетон Бора. g-фактор Ланде. Гиромагнитное отношение.
  • Энергия магнитного момента в магнитном поле.
  • Угловой момент в квантовой механике. Уровни энергии магнитного момента в постоянном магнитном поле в квантовой механике.
  • ЭПР свободного электрона с орбитальным угловым моментом равным 0.
  • Магнитный момент системы с ненулевыми орбитальным и спиновым моментами.
  • Уровни энергии иона хрома Cr3+ в кристалле рубина.
  • ЭПР кристалла рубина.
  • Спиновой гамильтониан.
  • Установка для наблюдения ЭПР.

Задание на дом

  1. Оценить отношение магнитного момента электрона в атоме водорода, имеющего орбитальное квантовое чило l=1 (спин не учитывать), к дипольному электрическому моменту. Считать радиус орбиты равным 1 ангстрему. Оценку провести в системе СГС, где обе величины имеют одинаковые размерности.
  2. Найти множитель Ланде для системы частиц для всех возможных полных моментов J, у которых суммарное орбитальное число L=3 и спиновое квантовое число S=3/2.
  3. Найти выражения для уровней энергии иона хрома Cr3+ в кристалле рубина для углов θ = 0 и 54,7356o (косинус от такого угла равен 1/√3). Разъяснения в конспекте лекций и ниже здесь.
    Упрощенный спиновой гамильтониан нижних уровней иона Cr3+ в рубине имеет вид:

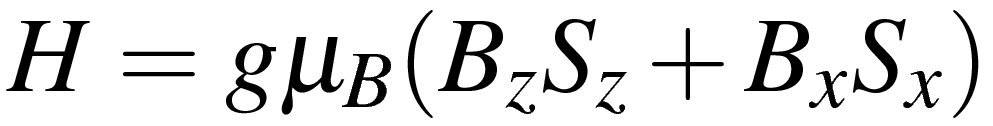
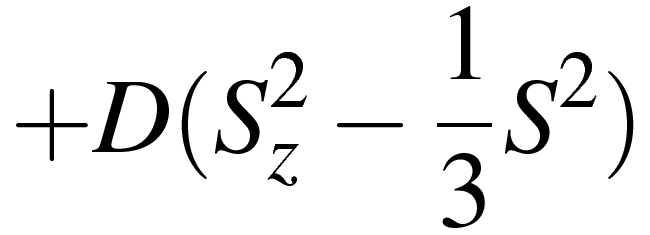
    Здесь g = 1,985 - фактор Ланде,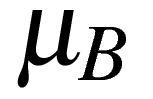 μ_B - магнетон Бора, D - постоянная кристаллического расщепления, равная -0,3831 см-1, B - индукция постоянного магнитного поля, Sz, Sx - компоненты эффективного спина. Ось z направлена вдоль оси симметрии кристалла, ось x перпендикулярно ей.
    Если ввести обозначение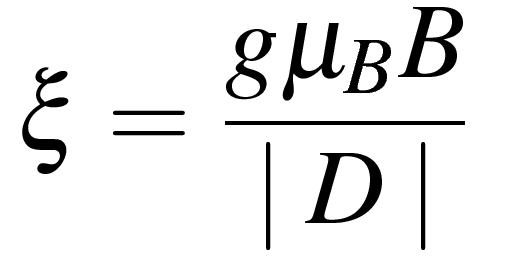 , а также определить угол θ между осью симметрии и направлением вектора индукции магнитного поля, то гамильтониан можно переписать в более простом виде:

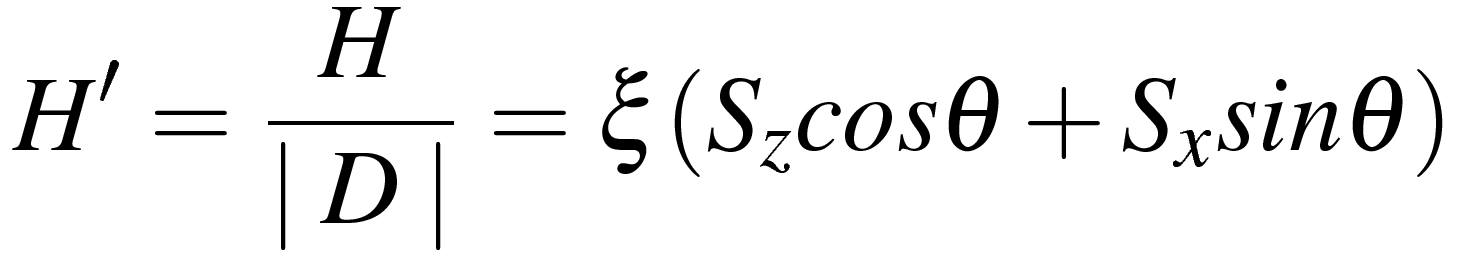
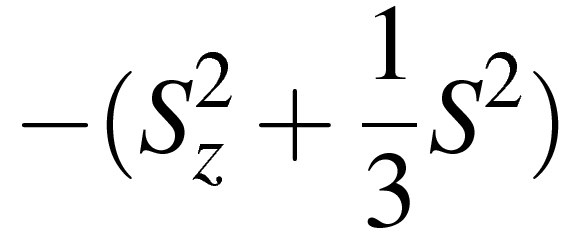
    При выводе выражений для уровней энергии (собственных значений гамильтониана) принять во внимание, что для иона Cr3+ значение квантового числа эффективного спина равно S=3/2, и что для такого числа матрицы компонент оператора спина, входящих в выражение для спинового гамильтониана, имеют вид:

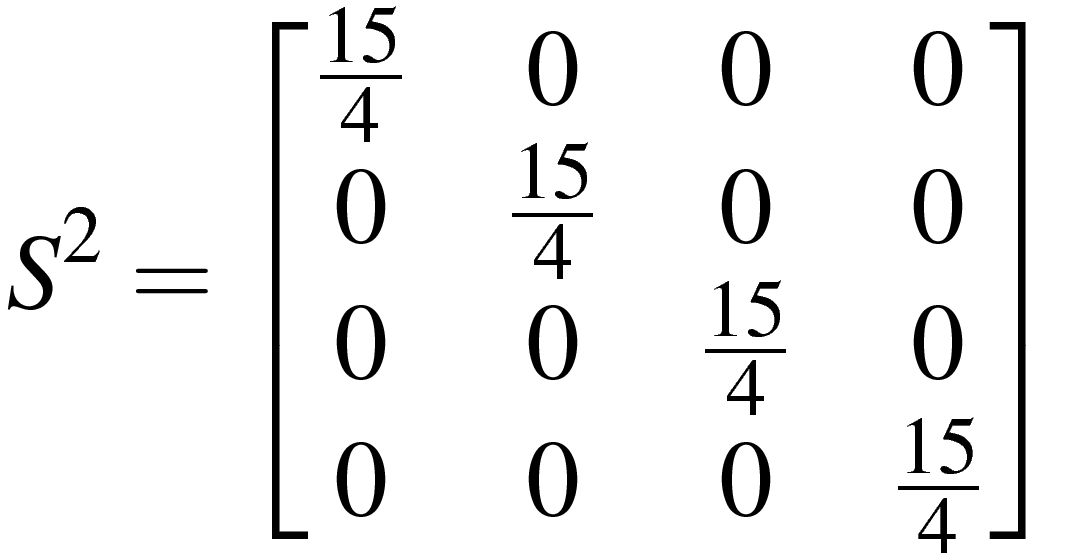
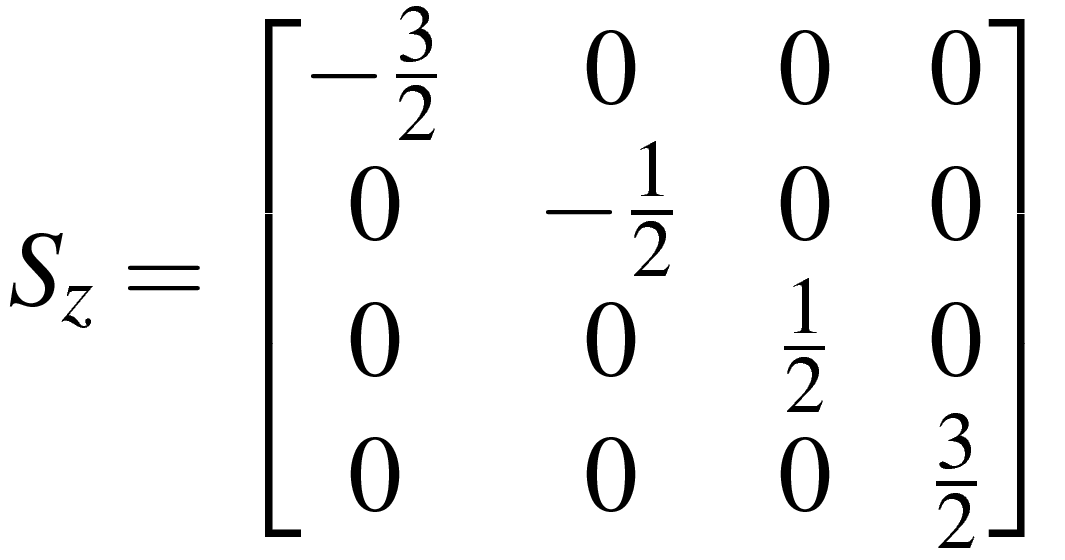
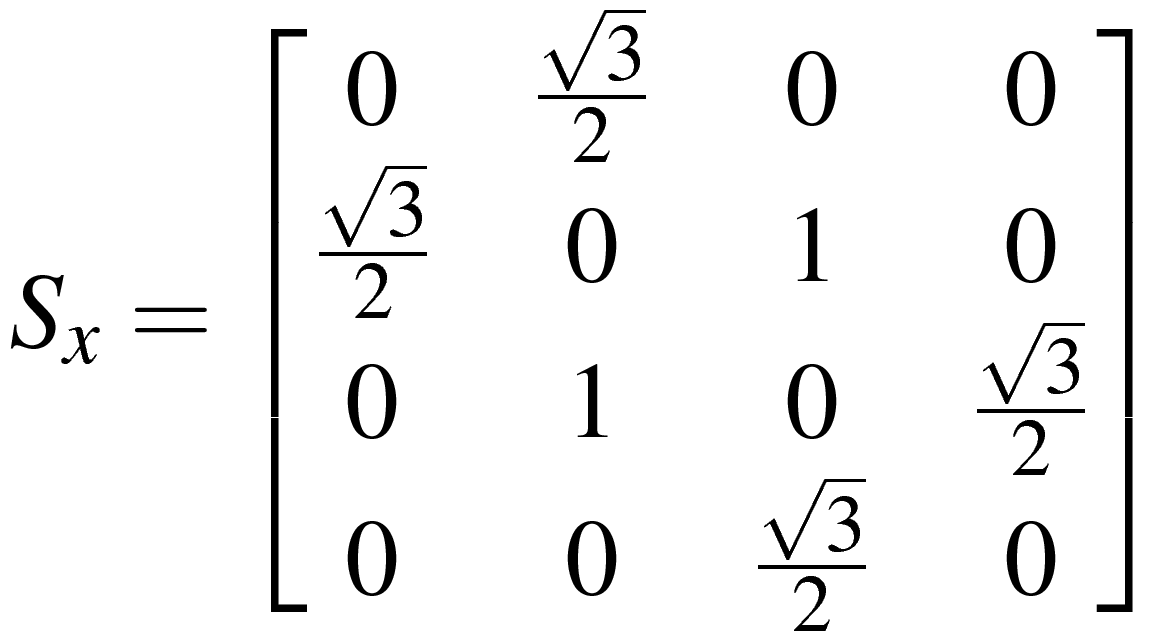
Литература

  1. В.М. Шульга, М.П. Перепечай, В.Б. Тютюнник, А.Н. Левченко. Квантовая радиофизика. Методические указания к лабораторным работам. 2010. Работы 1, 2.
  2. С.А. Песковацкий. Квантовая радиофизика. Текст лекций. 1984. Разделы 7.6, 7.7.
  3. С.А. Песковацкий, М.П. Перепечай, В.Б. Тютюнник. Методические указания к лабораторным работам по квантовой радиофизике. 1983. Раздел 3.1.
  4. Г.М. Страховский, А.В. Успенский. Основы квантовой электроники. 1973. Глава 3.
  5. В.И. Дудкин, Л.Н. Пахомов. Квантовая электроника. 2006. Глава 2.
  6. Г.М. Зверев, Ш.В. Карлов, Л.С. Корниенко, А.А. Маненков, А.Ш. Прохоров. Применение парамагнитных кристаллов в квантовой электронике. УФН, т. 77, вып. 1. с. 61-108. (1962).
  7. Л.А. Блюменфельд, А.Н. Тихонов. Электронный парамагнитный резонанс. Соровский образовательный журнал, №9, 1997.